Generic vanishing theorem I - Hacon’s approach

This is the first blog aim to introduce the generic vanishing theorem, follows Hacon’s proof. He use the Fourier-Mukai transform and something about Abelian varieties to solve this problem:

Main Theorem. Let $X$ be a smooth projective variety over $\mathbb{C}$. Let $a:X\to\mathrm{Alb}(X)$ be the Albanese map. Let \[S^i(\omega_X)=\{M\in A^t(\mathbb{C}): H^i(X,\omega_X\otimes M)\geq 0\},\] then $S^i(\omega_X)\subset A^t$ is closed of codimension $\geq i-\dim X+\dim a(X)$.

We follows from Hacon’s paper¹ and the original result due to Mark Green and Robert Lazarsfeld²³. We also refer Schnell’s notes lectures on generic vanishing theorem for the general discussion (and Generic vanishing seminar).

For the basic knowledge of Abelian varieties, we refer Bhargav Bhatt’s notes Abelian varieties and notes by his students TOPICS IN ALGEBRAIC GEOMETRY I – ABELIAN VARIETIES.

1. A glimpse of the theorem and Hacon’s proof

This theorem tell us that for general (whole space except some low dimensional closed sets) line bundle $L\in Pic^0(X)$, we have if $i<\dim(a(X))$, then $H^i(X,L)=H^{\dim X-i}(X,\omega_X\otimes L)=0$. If $a:X\to\mathrm{Alb}(X)$ is generically finite, then if $i>0$, then $H^{\dim X-i}(X,L)=H^i(X,\omega_X\otimes L)=0$.

Hacon’s proof using the Fourier-Mukai transform and some results of mixed Hodge theory (Kollar’s vanishing theorem) and we left this as a blackbox. Actually the most important thing is GV sheaf, as the last section in this blog.

2. A glimpse of Kollár’s vanishing theorem

This is the main step we use the characteristic zero.

Theorem 0. (Kollár⁴) If $f : X\to Y$ is a surjective map of projective varieties over $\mathbb{C}$ and $X$ is smooth, then

(i) for any ample line bundle $L$ on $Y$ , we have $H^i(Y,R^kf_* \omega_X\otimes L)=0$ for all $i>0$;

(ii) each $R^jf_* \omega_X$ is torsion-free; in particular, $R^jf_* \omega_X=0$ for $j>\dim X-\dim Y$;

(iii) there is decomposition $Rf_* \omega_X =\bigoplus_j R^jf_* \omega_X[-j]$ in $D(Y)$.

(Note that (iii) follows from mixed Hodge theory and BBD decomposition.)

3. Some notations

Fix $X$ be a smooth proper integral scheme over $\mathbb{C}$ of dimension $n$ and $A$ be an Abelian variety over $\mathbb{C}$ and $A^t$ be its duality.

(I) We denote $\mathbb{D}_X(-)=R\mathscr{H}om(-,\omega_X[n])$. Then by Grothendieck duality, if $f:X\to Y$ is a proper map between smooth, proper $\mathbb{C}$-schemes, then $Rf_* \circ\mathbb{D}_X\cong \mathbb{D}_Y\circ Rf_*$;

(II) We let $\Phi_A:=\Phi_{P_A}:D^b(A) \to D^b(A^t)$ be the Fourier-Mukai transform and $P_A$ be the Poincare bundle. Let $\phi_L:A\to A^t$ be the canonical map given by $x\mapsto t^* _x(L)\otimes L^{-1}$ where $L$ ample. Then one can show that when $L$ is ample over $A^t$, then $E(L):=\Phi_{A^t}(L)$ be a vector bundle and $\phi_L^* (\Phi_{A^t}(L))\cong H^0(A^t,L)\otimes L^{-1}$ (from the theory of non-degenerate line bundle, see Bhargav Bhatt’s notes Theorem 7.3.1 and Lemma 7.3.2).

4. GV complexes and GV sheaves

Fix $A$ be an Abelian variety of dimension $g$ over $\mathbb{C}$ and $A^t$ be its duality.

Definition - Theorem 4.1. (Hacon) If $F\in D^b_{coh}(A)$, the following are equivalent, we called it GV complex:

(i) The complex $\Phi_A(\mathbb{D}_A(F))\in D^{[0]}(A^t)$;

(ii) For $L$ sufficiently ample, we have $R\Gamma(A^t,\Phi_A(\mathbb{D}_A(F))\otimes L)\in D^{[0]}(Ab)$;

(iii) For $L$ sufficiently ample, we have $R\Gamma(A,F\otimes E(L)^{\vee})\in D^{[0]}(Ab)$;

(iv) $R\mathscr{H}om(\Phi_A(F),\mathscr{O}_{A^t})\in D^{[0]}(A^t)$;

(v) $\Phi_A(F)\cong R\mathscr{H}om(E,\mathscr{O}_{A^t})$ for some $E\in Coh(A^t)$.

Proof. For (ii) and (iii), just need to check the case after acting $\mathbb{D}_{\mathbb{C}}$ for (iii). By definitions and projection formula, one can get \[\mathbb{D}_{\mathbb{C}}(R\Gamma(A,F\otimes E(L)^{\vee}))\cong R\Gamma(A^t,\Phi_A(\mathbb{D}_{A}(F))\otimes L).\] Hence well done.

For (i) and (ii), consider the (Grothendieck-) spectral sequence \[E_2^{p,q}:H^p(A^t,\mathscr{H}^q(\Phi_A(\mathbb{D}_{A}(F)))\otimes L)\Rightarrow H^{p+q}(A^t,\Phi_A(\mathbb{D}_A(F))\otimes L).\] If we assume (i), then (ii) follows from Serre’s vanishing theorem. If we assume (ii), then for $L$ sufficiently ample, $H^n(A^t,\Phi_A(\mathbb{D}_A(F))\otimes L)=0$ for all $n>0$ and $H^p(A^t,\mathscr{H}^q(\Phi_A(\mathbb{D}_{A}(F)))\otimes L)=0$ for all $p>0$ and all $q\in\mathbb{Z}$, by Serre’s vanishing theorem. Hence the spectral sequence gives \[H^0(A^t,\mathscr{H}^q(\Phi_A(\mathbb{D}_{A}(F)))\otimes L)\cong H^{q}(A^t,\Phi_A(\mathbb{D}_A(F))\otimes L).\] Hence by $H^n(A^t,\Phi_A(\mathbb{D}_A(F))\otimes L)=0$ for $n>0$ we get $H^0(A^t,\mathscr{H}^q(\Phi_A(\mathbb{D}_{A}(F)))\otimes L)=0$ for $q\neq 0$. Hence if $\mathscr{H}^q(\Phi_A(\mathbb{D}_{A}(F)))\neq 0$ for $q\neq 0$, then taking $L$ so ample one can get the wrong way.

The equivalence of (iv) and (v) is trivial.

For (i) and (iv), we just need to show that \[\mathbb{D}_{A^t}(\Phi_A(F))\cong [-1]^* \Phi_A(\mathbb{D}_A(F))[g]\] as the canonical sheaf of Abelian varieties are trivial. One can show that $([a]\times[b])^* P_A\cong P_A^{\otimes ab}$ (left as an exercise). Hence $([1]\times[-1])^* P_A\cong P_A^{-1}$. Let $pr_i$ are projections from $A\times A^t$, then we have

\begin{align*} \mathbb{D}_{A^t}(\Phi_A(F))&\cong pr_{2,*}R\mathscr{H}om(pr_1^* F\otimes P_A,\mathscr{O}_{A\times A^t}[2g])\\ &\cong pr_{2,*}R\mathscr{H}om(pr_1^* F,([1]\times[-1])^*P_A[2g])\\ &\cong pr_{2,*}(pr_1^*\mathbb{D}_A(F)[g])\otimes([1]\times[-1])^*P_A\\ &\cong pr_{2,*}([1]\times[-1])^*(pr_1^*\mathbb{D}_A(F)[g])\otimes P_A \end{align*}

where the last isomorphism from $([1]\times[-1])\circ pr_1=pr_1$. Using the projection formula for the square ($f=[1]\times[-1]$):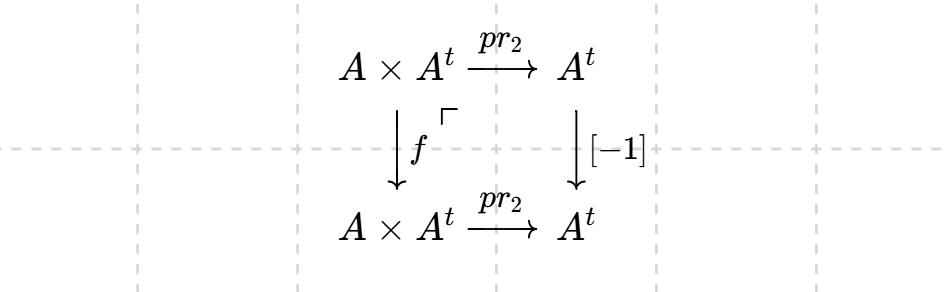

$$ \begin{xy} \xymatrix { A \times A^t \ar[d]^f \ar[r]^{pr_2} & A^t \ar[d]^{[-1]} \\ A \times A^t \ar[r]^{pr_2} & A^t } \end{xy} $$

we get $\mathbb{D}_{A^t}(\Phi_A(F))\cong [-1]^* \Phi_A(\mathbb{D}_A(F))[g]$, well done. $\blacksquare$

Here we need some lemmas of commutative algebra:

Lemma 1. If $F\in D^b_{coh}(A)$ is a GV complex, then $\mathrm{Supp}(\mathscr{H}^i(\Phi_A(F)))\subset A^t$ has codimension $\geq i$.

Proof. By Theorem 4.1 (v), we get $\Phi_A(F)\cong R\mathscr{H}om(E,\mathscr{O}_{A^t})$ for some $E\in Coh(A^t)$. Pick any point $x\in A^t$ of codimension $<i$, then $(\mathscr{H}^i(\Phi_A(F)))_x$ locally is $\mathrm{Ext}^i_{R_{\mathfrak{p}}}(M_{\mathfrak{p}},R_{\mathfrak{p}})$ where $R$ is regular and $ht(\mathfrak{p})<i$. As $gl.dim(R_{\mathfrak{p}})\leq\dim R_{\mathfrak{p}}<i$, well done. $\blacksquare$

Lemma 2. Let $R$ be a commutative ring and $M$ be a perfect complex. Then, for each integer $i$, we have \[S^i(R,M):=\{x\in\mathrm{Spec}(R):H^i(M\otimes_R\kappa(x))\neq 0\}\subset \bigcup_{j\geq i}\mathrm{Supp}(H^j(M))\] and it is cloed in $\mathrm{Spec}(R)$.

Proof. $S^i(R,M)$ is closed by the semicontinuity theorem. Furthermore, if the result does not hold, then $\exists x\in S^i(R,M)$ such that $H^j(M)\otimes_R R_x=0$ for all $j\geq i$. Hence $M\otimes_R R_x\in D^{<i}$, hecne so is $M\otimes_R R_x\otimes_{R_x}\kappa(x)=M\otimes_R \kappa(x)\in D^{<i}$. Hence $H^i(M\otimes_R\kappa(x))=0$. But this is impossible! $\blacksquare$

Lemma 3. Let $R$ be a noetherian local ring with $M$ a finitely generated $R$-module. If $\mathrm{Ext}^i_R(M,k)\neq0$ for some $i>0$, then $\mathrm{Ext}^{i-1}_R(M,k)\neq0$.

Proof. Pick a minimal free resolution $K^* $ of $M$, that is, each $K^i$ is finite free and the differential is $0$ modulo the maximal ideal of $R$. Hence if $\mathrm{Ext}^{i-1}_R(M,k)=0$, then $\dim_k\mathrm{Ext}^{i-1}_R(M,k)=rank(K^{i-1})=0$. By minimality and Nakayama’s lemma, $K^i=0$. But this is impossible! $\blacksquare$

This is the main theorem of this section:

Theorem 4.2. (Hacon-I) Let $F\in D^b_{coh}(A)$ be a GV complex.

(i) The cohomology support locus \[S^i(A^t,F):= \{M\in A^t(\mathbb{C}): H^i(A, F\otimes M)\neq 0\}\] is closed in $A^t$, and each irreducible component has codimension $\geq i$;

(ii) If $F$ is a GV sheaf (that is, a GV complex living in $Coh(A)$), then there is a sequence of inclusions $S^{j+1}(A^t,F)\subset S^{j}(A^t,F)$;

(iii) If $F$ is a GV sheaf, then $\chi(A,F)\geq 0$.

Remark. One can show that the condition in (i) can implies $F\in D^b_{coh}(A)$ be a GV complex, see Schnell’s notes Theorem 25.5. So many people define GV complex using the condition in (i).

Proof. (i) This is follows from Lemma 1 and Lemma 2 with $M=\Phi_A(F)$ (One can check that if $x\in A^t$ correspond to $M_x\in Pic^0(A)$, then $R\Gamma(A,F\otimes M_x)\cong\Phi_A(F)\otimes\kappa(x)$).

(ii) Just need to show that if $x=M\in A^t$ with $H^i(F\otimes M)\neq 0$, then $H^{i-1}(F\otimes M)\neq 0$. Let $\Phi_A(F)\cong R\mathscr{H}om(E,\mathscr{O}_{A^t})$, then \[R\mathscr{H}om(E,\kappa(x))\cong R\mathscr{H}om(E,\mathscr{O}_{A^t})\otimes \kappa(x)=\Phi_A(F)\otimes\kappa(x)= R\Gamma(A,F\otimes M).\] Hence (ii) follows from Lemma 3.

(iii) Easy to show that by (i) we get $\chi(A,F\otimes M)\geq 0$ from some degree $0$ line bundle $M$. As $\chi(A,F\otimes M)=\chi(A,F)$ since Euler characteristic is invariant via a flat family in $\underline{Pic}^0(X)=A^t$. $\blacksquare$

5. The main theorem

Fix $X$ be a smooth projective variety over $\mathbb{C}$ and $a:X\to\mathrm{Alb}(X)$ be the Albanese map. Let $A:=\mathrm{Alb}(X)$, then $A^t=\underline{\mathrm{Pic}}^0(X)$. Let $\dim A=g=h^1(X,\mathscr{O}_X)$.

Theorem 5.1. (Hacon-II) For any $k\in\mathbb{Z}_{\geq 0}$ we have $R^ka_* (\omega_X)$ is a GV sheaf.

Proof. Fix an ample line bundle $L$ over $A^t$, hence $\phi_L:A^t\to A$ is a finite etale cover and $\phi_L^* (E(L))\cong H^0(A,L)\otimes L^{-1}$. We need to show that $R\Gamma(A,R^ka_* (\omega_X)\otimes E(L)^{\vee})\in D^{[0]}$ when $L$ sufficiently ample. Now the map $\mathscr{O}_A\to (\phi_L)_* \mathscr{O}_{A^t}$ splitted by $\frac{tr(-)}{\deg(\phi_L)}$, hence we just need to show

\begin{align*} &R\Gamma(A,R^ka_* (\omega_X)\otimes E(L)^{\vee}\otimes (\phi_L)_* \mathscr{O}_{A^t}) \\ &\cong R\Gamma(A^t,\phi_L^* (R^ka_* (\omega_X))\otimes\phi_L^* (E(L)^{\vee}))\\ & \cong \bigoplus^{h^0(A,L)}R\Gamma(A^t,\phi_L^* (R^ka_* (\omega_X))\otimes L)\in D^{[0]}. \end{align*}

Consider the Cartesian diagram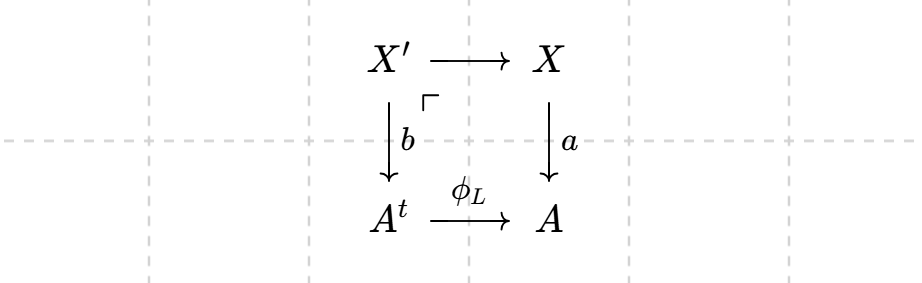

$$ \begin{xy} \xymatrix { X' \ar[d]^b \ar[r] & X \ar[d]^a \\ A^t \ar[r]^{\phi_L} & A } \end{xy} $$

As $\phi_L$ finite etale, one get $\phi_L^* (R^ka_* (\omega_X))=R^kb_* (\omega_{X’})$. Hence by Kollár’s vanishing theorem (Theorem 0 (i)), well done. $\blacksquare$

Recall that the main theorem:

Main Theorem. Let $X$ be a smooth projective variety over $\mathbb{C}$. Let $a:X\to\mathrm{Alb}(X)$ be the Albanese map. Let \[S^i(\omega_X)=\{M\in A^t(\mathbb{C}): H^i(X,\omega_X\otimes M)\geq 0\},\] then $S^i(\omega_X)\subset A^t$ is closed of codimension $\geq i-\dim X+\dim a(X)$.

Proof. By projection formula and $a:X\to A$ induce $\underline{Pic}^0(A)\cong \underline{Pic}^0(X)$, one get $S^i(\omega_X)=S^i(A^t,Ra_* (\omega_X))$. For any $M\in Pic^0(A)$, we have the (Grothendieck-) spectral sequence \[ E_2^{p,q}=H^{p}(A,R^qa_* (\omega_X)\otimes M)\Rightarrow H^{p+q}(A,Ra_* (\omega_X)\otimes M).\] Hence we get \[S^n(A^t,Ra_* (\omega_X))\subset\bigcup_p S^p(A^t,R^{n-p}a_* (\omega_X))\] for all $n\geq 0$. By Theorem 5.1, $R^ka_* (\omega_X)$ is a GV sheaf, hence by Theorem 4.2 (i) we get $codim(S^p(A^t,R^{n-p}a_* (\omega_X)))\geq p$. Hence just need to show if $S^p(A^t,R^{n-p}a_* (\omega_X))\neq\emptyset$, then $p\geq n-\dim X+\dim a(X)$. Now if $n-p>\dim X-\dim a(X)$, then by Kollár’s vanishing theorem (Theorem 0 (ii)) we get $R^{n-p}a_* (\omega_X)=0$. Well done. $\blacksquare$

6. Further results

6.1. Hacon’s more results

Hacon actually showed a more general result (a conjecture by Green-Lazarsfeld):

Theorem 6.1.1 (Green-Lazarsfeld conjecture). Let $X$ be a smooth complex projective variety, and let $P_X$ denote a universal line bundle on $X\times Pic^0(X)$. Then one has $R^ipr_{2,∗}P_X = 0$ for $i <\dim a(X)$.

Proof. See Schnell’s notes Theorem 26.1. If let $P_A$ be the Poincare bundle over $A\times A^t$, then one must has $P_X\cong(a\times id)^* P_A$. COnsider the Cartesian diagram: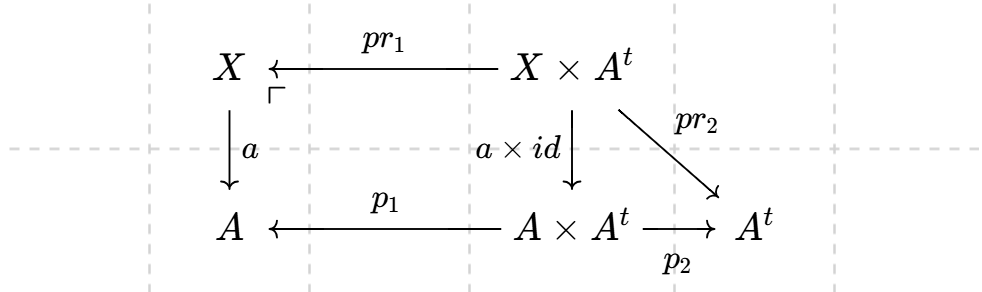

$$ \begin{xy} \xymatrix { X \ar[d]^a & X\times A^t \ar[l]^{pr_1} \ar[d]^{a\times id} \ar[dr]^{pr_2} &\\ A & A\times A^t \ar[l]^{p_1} \ar[r]^{p_2} & A^t } \end{xy} $$

By Grothendieck duality, projection formula and flat base change and $P_X\cong(a\times id)^* P_A$, we get

\begin{align*} &R\mathscr{H}om(Rpr_{2,* }P_X,\mathscr{O}_{A^t}) \\ &\cong Rp_{2,* }(P_A^{-1}\otimes p_1^* Ra_* \omega_X[\dim X]\\ &\cong \bigoplus_{j=0}^{\dim X-\dim a(X)}Rp_{2,*}(P_A^{-1}\otimes R^ja_*\omega_X)[\dim X-j]\\ &\cong \bigoplus_{j=0}^{\dim X-\dim a(X)}i^*\Phi_ARp_{2,*}(R^ja_*\omega_X)[\dim X-j]\\ &\cong \bigoplus_{j=0}^{\dim X-\dim a(X)}i^*R\mathscr{H}om(E_j,\mathscr{O}_{A^t})[\dim X-j]\\ \end{align*}

where the second isomorphism follows from Kollár’s vanishing theorem (Theorem 0.(iii)) and $i:A^t\to A^t$ be the inverse and the last step from the property of GV sheaves. Taking duality, one get \[Rpr_{2,* }P_X\cong\bigoplus_{j=0}^{\dim X-\dim a(X)}i^* E_j[j-\dim X].\] Taking cohomology and well done. $\blacksquare$

6.2. Furthermore about GV sheaves

The most surprising application of GV-sheaves is the birational characterization of abelian varieties by Chen and Hacon. Actually in the case of surfaces, the Enriques-Kodaira classification shows that a minimal smooth projective surface $S$ is abelian if and only if $\kappa(S) = 0$ and $q(S) = 2$. Here we have a version of higher dimension.

Theorem 6.2.1 (Chen-Hacon). Let $X$ be a smooth projective variety with $P_1(X) = P_2(X) = 1$ and $\dim H^1(X,\mathscr{O}_X) =\dim X$ where $P_m(X)=h^0(X,\omega_X^{\otimes m})$. Then $X$ is birational to an abelian variety, more precisely, $a:X\to A$ is birational.

Proof. See Schnell’s notes Theorem 27.3. They use the following criterion:

Pareschi’s criterion(Schnell’s notes Proposition 27.6) Let $X$ be a smooth projective variety of maximal Albanese dimension such that $\dim S^0(X, \omega_X) = 0$. Then $a:X\to A$ is birational.

6.3. Further results using mixed Hodge module

Actually the third statement of Kollár’s vanishing theorem proved by using BBD decomposition, or more precisely by its Hodge-theoretic version due to Morihiko Saito. This is one main reason why mixed Hodge modules form a natural setting here. Another is the existence of a very general Kodaira-type vanishing theorem for mixed Hodge modules, again due to Saito, which becomes particularly useful on abelian varieties. The more advanced we refer Mihnea Popa, Christian Schnell’s paper⁵.

First they shows a very complicated result about every mixed Hodge module on $A$ gives rise to a collection of sheaves satisfying the generic vanishing condition (Theorem 3.1). Using this one can show that:

Theorem 6.3.1 Let $X$ be a smooth complex projective variety of dimension $n$. Then \[codim S^q(\Omega_X^p)\geq |p+q-\dim X|-\max_{l\in\mathbb{Z}}\{2l-\dim X+\dim A_l\}\] where $A_l=\{y\in A:\dim a^{-1}(y)\geq l\}$. Moreover, there exists $p$ and $q$ for which this is an equality.

Proof. See paper⁵ Theorem 3.2.

There are much more results in this paper and we omit them here.