Some Remarks of the Kollar and Mori’s Birational Geometry of Algebraic Varieties II
Published:
This blog aim to give some remarks and complete some details in this book (Kollar and Mori’s Birational Geometry of Algebraic Varieties). I will read first five chapters of this book. This is the second blog which about chapter 3.
Previously on these:
Some Remarks of the Kollar and Mori’s Birational Geometry of Algebraic Varieties I.
Chapter 3. Cone Theorems
Section 3.2. Basepoint-free Theorem
Step 1. One may add that we find that log resolution with $\sum_j F_j(\supset\mathrm{Ex}(f)\cup\mathrm{supp}(f_* ^{-1}\Delta))$ is snc divisor. $\blacksquare$
Step 5. As $\sum_j F_j$ is snc, then $F$ is regular (hence smooth here). As $\sum(-cr_j+a_j-p_j)F_j=A-F$ for some $F=F_j$ with \[\min_j(-cr_j+a_j-p_j)=-1\] with unique such $j$ (is $F$), hence $\mathrm{discrep}(F,-A|_F)>-1$ by Corollary 2.31. Hence $(F,-A|_F)$ is a klt pair. $\blacksquare$
Section 3.3. The Cone Theorem
Step 3. Let \[W=\mathrm{closure}\left(\overline{NE}_{K\geq 0}+\sum_{\dim F_L=1}F_L\right)\] and pick such $M\in N_{\mathbb{Z}}^* $ such that $F_M\neq\emptyset$ and $F_M\cap W=\emptyset$ with taking positive value over $W$. Let $\mu$ be the largest such that $H+\mu M$ is nef, then it is not ample with $z\cdot(H+\mu M)=0$ and $z\cdot K<0$. Hence $F_{H+\mu M}$ is not contained in $\overline{NE}_{K\geq 0}$. By Step 2 we get a nef $L$ such that $F_L\subset F_{H+\mu M}$ with $\dim F_L=1$ which is impossible! $\blacksquare$
Step 4. Actually we get quotient $(K<0)\to U\subset\mathbb{P}(N_{\mathbb{R}})$ by $\xi\mapsto [(\xi\cdot K):(\xi\cdot H_1):\cdots :(\xi\cdot H_d)]$ and we showed these $F_L$ is discrete in $U$. Now as $\mathbb{P}(\overline{NE}_{k+\varepsilon H\leq 0})\subset U$ is compact and hence contained finite number of these $F_L$ and so is in $\mathbb{P}(\overline{NE}_{k+\varepsilon H< 0})$. $\blacksquare$
Corollary 3.17, 3.18. We may add $\Delta\geq 0$. $\blacksquare$
Corollary 3.18. The first $E\cdot R\neq0$ follows from the following lemma from L3:
Negativity Lemma. Let $X\to Y$ be a birational projective morphism between normal varieties. If $E$ is any exceptional divisor such that $−E$ is nef, then $E\geq 0$. In particular if $E\geq 0$ is exceptional then $E$ is nef if and only if $E = 0$. $\blacksquare$
Add a new corollary! Let $(X,\Delta)$ is a projective klt pair and $F\subset\overline{NE}(X)$ be a $(K_X+\Delta)$-negative extremal face with contraction $g_F:X\to Z$. Then in derived category we have $Rg_{F,* }\mathscr{O}_X\cong\mathscr{O}_Z$.
Proof. We just show that $R^ig_{F,* }\mathscr{O}_X=0$ for $i>0$. As $-(K_X+\Delta)$ is $g_F$-ample, by relative Kawamata–Viehweg vanishing theorem for klt pairs (see Lecture15) well done. $\blacksquare$
Section 3.4. The Rationality Theorem
Step 1. We need to check that the new $H’$ is also nef and big! Here we need to choose appropriate coefficients $m\gg c\gg d > 0$. First we let $r(H)>0$ (or the theorem is obvious), then $H’$ is big by the openness of bigness when $c\gg d > 0$. For the nefness, we may let $n\in\mathbb{N}$ with $H+\frac{1}{n}(K_X+\Delta)$ is nef, hence so is $naH+a(K_X+\Delta)$. As $nH=nH+(K_X+\Delta)-(K_X+\Delta)$ is nef and big, by basepoint-free theorem the linear series $|b(naH+a(K_X+\Delta))|$ is free. Let $d=1,m=b,c=na$ and well done. $\blacksquare$
Step 4. Here we deal with this claim: Claim. For $(p,q)$ sufficiently large and $0 < aq-rq < \varepsilon$, then $L(p,q):=\mathrm{Bs}(|pH+qa(K_X+\Delta)|)$ stable.
The diagram here is not very clear, which leads me astray. Here I redraw a new clearer diagram:
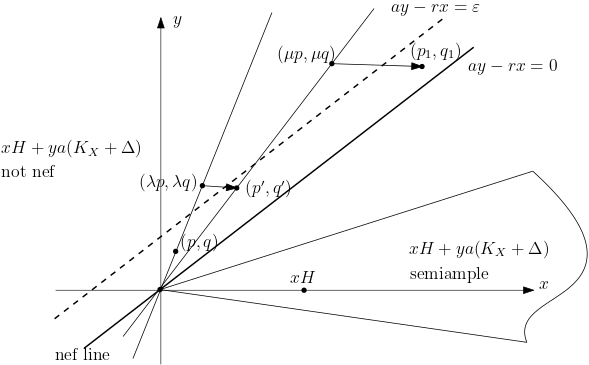
We need to go through the following process with this diagram:
(I) First, pick some $(p,q)$ in the strip. If $(p’,q’)$ large enough, then one can take $(\lambda p,\lambda q)$ and draw an arrow to $(p’,q’)$. Note that $xH$ is semiample now! Hence we can let the direction of this arrow in that semiample cone and the length of the arrow is base-point free! Hence \[p’H+q’a(K_X+\Delta)=\lambda pH+\lambda qa(K_X+\Delta)+\mathrm{free}.\] As $L(\lambda p,\lambda q)\subset L(p,q)$, we get $L(p’,q’)\subset L(\lambda p,\lambda q)\subset L(p,q)$.
(II) Second, let $(p_1,q_1)$ far from $(p’,q’)$ and do the same thing in the first step, then we get $L(p_1,q_1)\subset L(p’,q’)$. Repeat this and using the Noetherian condition, we get a sequence of stable base locuses equal to $L_0$.
(III) Finally, pick two adjacent pairs $(p_n,q_n)$ and $(p_{n+1},q_{n+1})$ in (II) with stable base locuses $L_0$. Hence for any $(p_0,q_0)$ in the strip larger than $(p_{n+1},q_{n+1})$, we can do the same process in (I) with $(p_n,q_n)$ and $(p_0,q_0)$ and get $L(p_0,q_0)=L_0$. So we can let $(p_{n+1},q_{n+1})$ be the thresfold of sufficiently large in the Claim! Well done! $\blacksquare$
Section 3.5. The Non-vanishing Theorem
Step 2. They claim that the number of conditions on $M(q,e)\in|e(qD+G-K_X)|$ that $\mathrm{mult}_x M(q,e)>2de$ is at most \[\frac{e^d}{d!}(2d)^d+\mathcal{O}(e^{d-1}).\]
In the original paper: Actually consider the blowing up $\mathrm{Bl}_xX\to X$ with exceptional divisor $E\cong\mathbb{P}^{d-1}$. Therefore, passing through $x$ imposes $1$ condition, passing through $x$ with multiplicity $2$ imposes a further $d$ conditions,…, and passing through $x$ with multiplicity $l$ imposes a further $\binom{l+d-2}{d-1}$ conditions. Therefore passing through $x$ with multiplicity $l$ imposes a total of $\binom{l+d-1}{d}$ conditions.
Now I will give a more clear explanation of these (taken from birgeom): Let $D$ be a Cartier divisor on a smooth variety $X$, and $x\in X$ a point. Moreover, suppose that $\{h_1,…,h_n\}$ is a basis of $H^0(X,D)$ over $\mathbb{C}$. So $\forall h\in H^0(X,D)$ we have unique expression $h=\sum_i a_ih_i$ where we can assume that all the $h_i$ are regular at $x$ (maybe after changing $D$ in its linear system). So, $h_i$ can be described as polynomials in $d$ variables $t_1, . . . , t_d$ near $x$. Thus, to give $(h)_0=(h) + D\geq 0$ of multiplicity $>l$ at $x$ is the same as giving $h$ with multiplicity $>l$ with respect to $tj$. In particular, we have at most \[\sharp\{\deg \mathrm{monomials}\leq l\}=\frac{l^d}{d!}+\mathcal{O}(l^{d-1})\] conditions to check. That is, there at most codimension $\frac{l^d}{d!}+\mathcal{O}(l^{d-1})$ in $H^0(X,D)$ mains multiplicity $>l$. $\blacksquare$
Section 3.7. Running the MMP
A comment of 3.31.2.(1). Let $f:X\to Y$ be a projective contraction between normal varieties with $\rho(X/Y) = 1$. Assume that the exceptional locus of $f$ contains a divisor, then $f$ is the contraction of a unique irreducible divisor. See MMP Lemma 2.5.7 for the proof. $\blacksquare$
A comment of 3.31.2.(2). If we get a $(K_X+\Delta)$-flipping contraction $f:X\to Y$, why we need to get the flip $f^+:X^+\to Y$ instead of $(Y,f_* \Delta)$? Actually in this case $K_Y+f_* \Delta$ is not $\mathbb{Q}$-Cartier! Indeed, if it is, as $K_X+\Delta=f^* (K_Y+f_* \Delta)$ as $f$ is small, then we have some $f$-contracted curve $l$ such that \[0>(K_X+\Delta)\cdot l=f^* (K_Y+f_* \Delta)\cdot l=0\] which gives a contradiction! $\blacksquare$
Lemma 3.38. The proof after the Lemma 3.41. After taking the complete intersection $S$ of $n-2$ hypersurfaces in normal affine variety $Y$, they claim that $S$ is again a normal surface. Why? Actually this follows from the following results taken from Theorem 3.2 in Arxiv:1912.09076:
Theorem. (Bertini type theorem for normality). Assume that $X$ is an $(R_a +S_b)$-scheme over infinite field $k$ for some $a, b\geq 0$ and $Z\subset\mathbb{P}^n_k$ be a closed subscheme such that $Z\cap X$ is a reduced finite subscheme contained in $X_{reg}$. Then there exists a general hypersurface $H\subset\mathbb{P}^n_k$ containing $Z$ satisfies $X_{reg}\cap H$ is regular and $X\cap H$ is an $(R_a +S_b)$-scheme.
Then using the $R_1+S_2$ for normality, well done! $\blacksquare$
Lemma 3.40. They claim that $H^0(Y,\mathscr{O}_Y(nD+H))\subset H^0(X,\mathscr{O}_X(f_* (nD+H)))$ where $D$ be a combination of exceptional divisors of a resolution $f:Y\to X$. Let $F:=nD+H$ and let $f|_{Y^0}:Y^0\to X^0$ be the isomorphism, then we have
\begin{align*} H^0(Y,\mathscr{O}_Y(F))&=\{g\in K(Y):F+(g)\geq 0\}\\ &\subset\{g\in K(Y^0):F|_{Y^0}+(g)\geq 0\}\\ &=\{g\in K(X^0):F|_{X^0}+(g)\geq 0\}\\ &=\{g\in K(X):f_*F+(g)\geq 0\}\\ &=H^0(X,\mathscr{O}_X(f_*F)), \end{align*}
well done. $\blacksquare$
More on Lemma 3.40. Let $f:X\dashrightarrow Y$ be a small birational map of normal varieties and $D$ a Weil divisor, then $f_* \mathscr{O}_X(D)\cong\mathscr{O}_Y(f_* D)$. In particular $H^0(\mathscr{O}_X(D))\cong H^0(\mathscr{O}_Y(f_* D)$.
Indeed, we just need to show $H^0(\mathscr{O}_X(D))\cong H^0(\mathscr{O}_Y(f_* D)$. We just deal with the line bundle case. Locally this is just Hartogs’s theorem. To gluing them up, we find that locally the restriction map on $\mathscr{O}_U$ to a dense open subset is always injective as it is integral and the sections of $\mathscr{O}_X$ can be viewed as morphisms to $\mathbb{A}^1$ and the latter is separated (hence we get the uniqueness of the maps)! Well done.
Of course we can do it directly for the general case as previous method. $\blacksquare$
A fundamental result about the flips. Let $f:X\to Y$ be a flipping contraction for a dlt pair $(X,\Delta)$ with $\mathbb{Q}$-divisor $\Delta$. The flip $f^+$ exists, if and only if $\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)$ is a finitely generated $\mathscr{O}_Y$-algebra. We then have that \[X^+ \cong\underline{\mathrm{Proj}}_Y\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor).\]
Proof. If the flip $f^+$ exists we get $X\dashrightarrow X^+$ is small and $K_{X^+}+\Delta^+$ is $f^+$-ample, then we get \[\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)\cong\bigoplus_{m\geq 0} f^+_* \mathscr{O}_{X^+}(\lfloor m(K_{X^+}+\Delta^+)\rfloor)\] and the right-hand side is a finitely generated sheaf of $\mathscr{O}_Y$-algebras. Finally we have $X^+ \cong\underline{\mathrm{Proj}}_Y\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)$ as it is proper.
Conversely, let $\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)$ is a finitely generated $\mathscr{O}_Y$-algebra. Let $X^+:=\underline{\mathrm{Proj}}_Y\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)$ and claim that $f^+:X^+\to Y$ is the flip. Here we just give a sketch and we refer Proposition 5.21 in [CHDAV10]1 or Theorem 9-1-2 in [Mori02]2. WLOG we let $K_X+\Delta$ is of integral coeffecient as it is $\mathbb{Q}$-divisor. If $E$ is a $f^+$-exceptional divisor and as for some $m\gg0$ we have \[f^+_* \mathscr{O}_{X^+}(1)\cong f_* \mathscr{O}_X(m(K_X+\Delta))\cong \mathscr{O}_Y(m(K_Y+f_* \Delta)),\] hence for any $t\gg0$ we get\[\mathscr{O}_Y(tm(K_Y+f_* \Delta))\cong f^+_* \mathscr{O}_{X^+}(t)\subset f^+_* \mathscr{O}_{X^+}(t)(E)\] where the last inclusion is strict. As $E$ is $f^+$-exceptional and sheaf $\mathscr{O}_Y(tm(K_Y+f_* \Delta))$ is reflexive. Hence $f^+$ is small. Others are omitted. $\blacksquare$
More Things. Bhatt and Lurie proved a version of the Riemann-Hilbert correspondence in positive characteristic. Bhatt proved the Cohen-Macaulayness of the integral closure of an excellent Noetherian domain. Using these techniques and results, MMP has recently been generalized in two different directions:
- In dimension $3$ in mixed characteristic (essentially over $\mathrm{Spec}\mathbb{Z}$) by Bhatt-Ma-PatakfalviSchwede-Tucker-Waldron-Witaszek;
- In characteristic $0$, most of the MMP works over an excellent $\mathbb{Q}$-scheme by Murayama-Lyu. $\blacksquare$
Section 3.8. Minimal and Canonical Models
Corollary 3.53. Here we explain how we use effectivity of $E$. Here we follows Lemma 7.11 and some comments in 7.12 in [HDAG01]3.
- Let $f:X\to Y$ be a proper birational map between varieties with $Y$ normal. Let $D$ be a Cartier divisor on $Y$ and $E$ is effective $f$-exceptional divisor on $X$, then we have $H^0(Y,D)\cong H^0(X,f^* D+E)$. Hence in particular we have $f_* \mathscr{O}_X(E)\cong\mathscr{O}_Y$.
Proof. As we have \[H^0(Y,D)\subset H^0(X,f^* D)\subset H^0(X,f^* D+E)\subset H^0(X\backslash\mathrm{Ex}(f),f^* D+E)\] and isomorphisms \[H^0(X\backslash\mathrm{Ex}(f),f^* D+E)\cong H^0(X\backslash\mathrm{Ex}(f),f^* D)\cong H^0(Y\backslash f(\mathrm{Ex}(f)),D)\cong H^0(Y,D)\] as $\mathrm{codim}_Yf(\mathrm{Ex}(f))\geq2$. Hence well done. $\blacksquare$
Remark. (1) For some kind of converse, see the comments of Corollary 5.24 in KMIII;
(2) I don’t know whether this lemma is right for general divisor $D$ or not. Actually I’m not sure if the projection formula holds for reflexive rank $1$-module (or more precisely, injective object tensoring a reflexive rank $1$-module is always an injective object?). $\blacksquare$
Corollary 3.54. Here by (3.53) we can get $X_i$ are canonical models of $K_{X_i}$ are $f_i$-ample, respectively. But why we assume $f_i$-nef and $X_i$ is of minimal model by (3.53)? I don’t know what’s going on.