Some Remarks of the Kollar and Mori’s Birational Geometry of Algebraic Varieties III (The End)

This blog aim to give some remarks and complete some details in this book (Kollar and Mori’s Birational Geometry of Algebraic Varieties). I will read first five chapters of this book. This is the third blog which about chapter 4 and chapter 5.

Previously on these:

Some Remarks of the Kollar and Mori’s Birational Geometry of Algebraic Varieties I;

Some Remarks of the Kollar and Mori’s Birational Geometry of Algebraic Varieties II.

Chapter 4. Surface Singularities of the Minimal Model Program

Section 4.1. Log Canonical Surface Singulariries

Theorem 4.5. Here I need to point out that when the case $(X,\Delta)$ canonical and not smooth, then $E\neq\emptyset$ and $E=\bigcup_i E_i$ with negative definite $(E_i\cdot E_j)$. Then by proof of the minimal model of surface Theorem 1.28 (kill the $(-1)$-curves), we find that $K_Y$ is nef! $\blacksquare$

Section 4.2/4.3. Du Val Singularities and Its Simultaneous Resolutions

Theorem 4.20. What is a surface double point? I will omit this. Second, in the proof of Du Val singularity implies canonical, we use a fact taken from Tag 0AV9:

Lemma. Let $R$ be a Noetherian domain. Let $f:M\to N$ be a map of $R$-modules. Assume $M$ is finite, $N$ is torsion free, and that for every prime $\mathfrak{p}$ of $R$ one of the following happens:

(I) $M_{\mathfrak{p}}\to N_{\mathfrak{p}}$ is an isomorphism, or

(II) $\mathrm{depth}(M_{\mathfrak{p}})\geq 2$.

Then $f$ is an isomorphism.

Now we get map $f_* \mathscr{O}_Y(K_Y)\to \mathscr{O}_X(K_X)$ which is isomorphism outside $0$ and $\mathscr{O}_X(K_X)$ is torsion free since it is reflexive. Over $0:=\mathfrak{p}_0$ we have $\mathrm{depth}(M_{\mathfrak{p}_0})=\mathrm{depth}(R_{\mathfrak{p}_0})\geq 2$ by normality ($S_2$). Hence $K_X$ is Cartier and hence by the same reason, we get $f^* \mathscr{O}_X(K_X)\cong \mathscr{O}_Y(K_Y)$. $\blacksquare$

I will omit the whole proofs in section 4.2 and 4.3 for now and I will read it when I need or want to read it…

Section 4.4. Elliptic Surface Singularities

Proposition 4.45. For the proof of (3), we find a section of $L$ generates $L$ near $E$ and $L\equiv_f0$, then why $L\cong\mathscr{O}_Y$?

Proposition 4.47. For the final step of the first paragraph, why $\omega_Y(Z)\cong\mathscr{O}_Y$? For the first sentence of the second paragraph, why $f^* \mathscr{O}_X(K_X)\cong\mathscr{O}_Y$ when $K_X$ Cartier?

Theorem 4.57. In step 4, why $K_{B^* X}=p_* K_Y$ and $K_{Y}=p^* K_{B^* X}$? In step 5, why when $k=2$ the $B^* X$ is the normalization of blowing up?

Chapter 5. Singularities of the Minimal Model Program

Geography of singularities: The geography of singularity types with implications looks like this:

Section 5.1. Rational Singularities

Definition 5.2. For the fact that over normal scheme a torsion free sheaf $F$ is $S_2$ iff it is reflexive, we refer the proof in Tag 0AVB. $\blacksquare$

Lemma 5.12. We may let $Y$ is a normal variety in this proof. Moreover, we can give a simply proof of (2) implies (1) as follows (taken from [RatKovacs00]¹ Lemma 1, seems without using the normality):

Proof. GR vanishing Theorem told us that $\omega_Y\simeq Rf_* \omega_X$, hence by Grothendieck duality we get

\begin{align*} \mathscr{O}_Y&\simeq R\mathscr{H}om_Y(\omega_Y,\omega_Y)\simeq R\mathscr{H}om_Y(Rf_* \omega_X,\omega_Y)\\ &\simeq Rf_*R\mathscr{H}om_X(\omega_X,\omega_X)\simeq Rf_*\mathscr{O}_X \end{align*}

well done. $\blacksquare$

For more things, a more advanced results about rational singularities we refer [RatKovacs17]², and papers [RatKovacs00]¹, [Dais02]³ (Theorem 1.4) and [Kol96]⁴ (section 11) are also introduced some results about rational singularities. $\blacksquare$

Proposition 5.13. For the final step, we need to use the following result: if $f:Y\to X$ be a resolution of singularities ($X$ normal) with $E=f^{-1}(\mathrm{Sing}(X))$ and natural inclusions $\iota: \mathrm{Reg}(X)\to X$, $j:Y\backslash E\to Y$. Consider the diagram: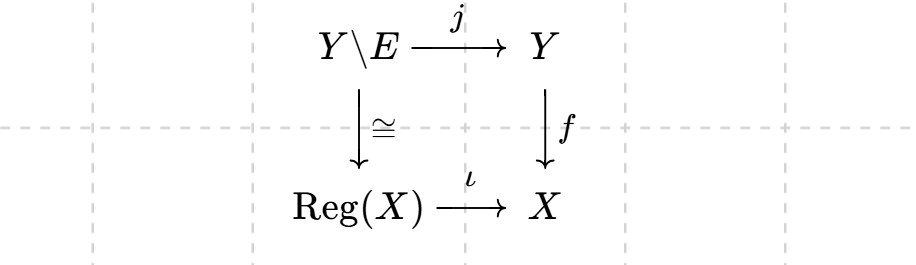

$$ \begin{xy} \xymatrix { Y\backslash E \ar[d]^{\cong} \ar[r]^j & Y\ar[d]_f \\ \mathrm{Reg}(X) \ar[r]^{\iota} & X } \end{xy} $$

Hence we have

\begin{align*} f_*\omega_Y&\hookrightarrow f_*j_*j^*\omega_Y=\iota_*\omega_{\mathrm{Reg}(X)}=\omega_{X} \end{align*}

which is an injection, well done. $\blacksquare$

Section 5.2. Log Terminal Singularities

Lemma 5.17. How to use (2.32) to deduce (2)?

Proposition 5.20.(1)(2)(3)/Corollary 5.21. For the some details in the proofs of these, we refer the whole section 2.3 in [Kol13]⁵! For example, 2.40 for (1) and 2.41-2.42 for (2)(3) and 2.49-2.51 for Corollary 5.21. $\blacksquare$

Corollary 5.24. Here we use some kind of converse of comments of Corollary 3.53 in KMII, taken from 7.12 in the book [HDAG01]⁶:

Lemma. If $f:Y\to X$ is proper birational where $X$ is normal and $Y$ is normal which satisfied that any Cartier divisor can be the difference of two effective Cartier divisors with no common component. Then for any exceptional Cartier $F$ in $Y$, we have $f_* \mathscr{O}_Y(F)\cong\mathscr{O}_X$ if and only if $F$ effective.

Proof. Let $F=F_1-F_2$ be the difference of two effective Cartier divisors with no common component. Hence $f_* \mathscr{O}_Y(F)\subset f_* \mathscr{O}_Y(F_1)\cong\mathscr{O}_X$. It is therefore a sheaf of ideals that defines a subscheme of $X$ supported on $f(F_2)$, follows from the definition of the ideal sheaf of the scheme-theoric image. Well done. $\blacksquare$

Remark. (i) For the condition of $Y$ in Lemma, we can not always have, but if $Y$ admits an ample line bundle or using the Fulton’s trick (after some blowing up of ideal of denominators, in the proof in Section 2.4 of his famous book), we can get it.

(ii) We have more interesting things like these:

From [KMM87]⁷ Lemma 1-3-2, we have the following result due to Fujita, aiming to prove the vanishing theorem of Elkik and Fujita:

[Lemma] If $f:Y\to X$ be a proper birational map from a smooth variety $Y$ onto $X$. Let $L,E$ be the Cartier divisor on $Y$ and $D$ is a $\mathbb{Q}$-Cartier divisor on $Y$. Assume that the support of $D$ is a divisor with only simple normal crossings, $\lfloor D \rfloor=0$, $-L-D$ is $f$-nef, and that $E$ is effective and exceptional for $f$. Then $f_* (\mathscr{O}_E(L+E))=0$.

Now we consider the case: if$f:Y\to X$ be a proper birational map from a smooth variety $Y$ onto a normal variety $X$, Let $P,N$ effective on $Y$ without common components and $P$ is exceptional for $f$. We claim that $f_* \mathscr{O}_Y(P-N)=f_* \mathscr{O}_Y(-N)$.

Indeed, use this Lemma to $L=D=0$ and $E=P$, then $f_* \mathscr{O}_P(P-N)\subset f_* (\mathscr{O}_P(P))=0$. Consider the exact sequence $0\to f_* \mathscr{O}_Y(-N)\to f_* \mathscr{O}_Y(P-N)\to f_* \mathscr{O}_P(P-N)=0$. Hence $f_* \mathscr{O}_Y(P-N)=f_* \mathscr{O}_Y(-N)$. Well done.

Section 5.4. Inversion of Adjunction

Proposition 5.46/Remark 5.47. Not that the condition that $S$ is Cartier in codimension $2$ aiming to use the adjunction formula (see Remark 5.47). For some more general case this needs some correction terms. Here we refer [JK92]⁸ section 16 (and section 17 is the conclusions of inversion of adjunction) and more advanced [Kol13]⁵ chapter 4 (or more precisely, section 4.1). $\blacksquare$

Corollary 5.52. We may let $X$ quasi-projective in order to use the Proposition 2.43. $\blacksquare$