Projections from the Subspaces of Projective Spaces

Here we give some detailed construction about the projections from the subspaces $\mathbb{P}(V/W)$ of projective spaces $\mathbb{P}(V)\backslash \mathbb{P}(V/W)\to\mathbb{P}(W)$. We follows notes Math 732: Topics in Algebraic Geometry II and Math 732. Rationality of algebraic varieties.

Here we fix some field $k$ and doing geometry over it.

Consider a projective space $\mathbb{P}(V)$ with an exact sequence \[0\to W\to V\to V/W\to 0.\] This induce a rational map

which called the projection with center $\mathbb{P}(V/W)$.

Remark. Geometrically, one can choose a splitting of $W\hookrightarrow V$ which gives $\mathbb{P}(W)\hookrightarrow \mathbb{P}(V)$ such that $\mathbb{P}(W)\cap \mathbb{P}(V/W)=\emptyset$. The $\phi$ maps $p$ into the linear span of $p$ and $\mathbb{P}(V/W)$ in $\mathbb{P}(W)$! In coordinates, if $\mathbb{P}(W)=V_+(x_{r+1},…,x_n)$ and $\mathbb{P}(V/W)=V_+(x_{0},…,x_r)$, then $\phi(x_{0},…,x_n)=(x_{0},…,x_r)$.

Our goal is following:

Main Goal. Consider the blowing up: Then the lifting realizes $\mathrm{Bl}_{\mathbb{P}(V/W)}\mathbb{P}(V)$ as a projective bundle $\mathbb{P}(\mathscr{E})$ over $\mathbb{P}(W)$ and we need to describe this $\mathbb{P}(\mathscr{E})$ and use this to find the exceptional divisor of this blowing up.

Fix a splitting of $W\hookrightarrow V$ which gives $V\cong W\oplus V/W$. Consider the bundle \[\mathscr{E}:=\mathscr{O}_{\mathbb{P}(W)}(1)\oplus(V/W\otimes \mathscr{O}_{\mathbb{P}(W)}).\] Consider $g:B:=\mathbb{P}(\mathscr{E})\to \mathbb{P}(W)$ with $\mathscr{L}:=\mathscr{O}_B(1)$. Easy to see that $\mathscr{E}$ generated by global sections and \[H^0(\mathbb{P}(W),\mathscr{E})\otimes\mathscr{O}_{\mathbb{P}(W)}\cong (H^0(\mathscr{O}_{\mathbb{P}(W)}(1))\oplus V/W)\otimes\mathscr{O}_{\mathbb{P}(W)} =V\otimes \mathscr{O}_{\mathbb{P}(W)}.\] This induce the following diagram: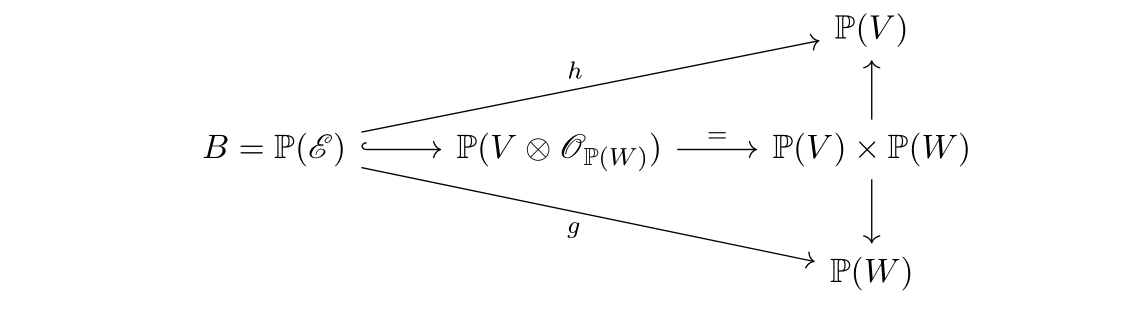

Proposition 1. We have $h^* \mathscr{O}_{\mathbb{P}(V)}(1)\cong\mathscr{L}$, hence $h$ is the morphism defined by $\mathscr{L}=\mathscr{O}_B(1)$ and the surjection \[H^0(B,\mathscr{L})\otimes\mathscr{O}_B=H^0(\mathbb{P}(W),\mathscr{E})\otimes\mathscr{O}_B=V\otimes\mathscr{O}_B\twoheadrightarrow \mathscr{L}.\]

Proof. Easy to see. Omitted. $\blacksquare$

Consider surjection $\mathscr{E}\twoheadrightarrow V/W\otimes\mathscr{O}_{\mathbb{P}(W)}$ which induce $E:=\mathbb{P}(V/W)\times\mathbb{P}(W)\hookrightarrow B$ which is a projective subbundle. Easy to see that $E$ is a smooth irreducible divisor in $B$. We also have $\mathscr{L}|_{E}\cong \mathrm{pr}_1^* \mathscr{O}_{\mathbb{P}(V/W)}(1)$ and the following commutative diagram 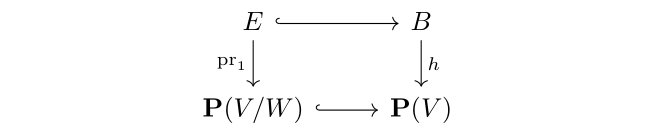Actually we have the following result:

Lemma 2. In this case we have $h^{-1}(\mathbb{P}(V/W))=E$.

Proof. Consider the following well-known fact:

Fact. Surjection $\psi:\mathscr{E}_1\twoheadrightarrow\mathscr{E}_2$ over some scheme $Y$ induce $\mathbb{P}(\mathscr{E}_2)\hookrightarrow\mathbb{P}(\mathscr{E}_1)$ as a closed subscheme defined by the zero locus of \[\pi^* (\ker\psi)\hookrightarrow\pi^* \mathscr{E}_1\twoheadrightarrow\mathscr{O}_Y(1)\] where $\pi:\mathbb{P}(\mathscr{E}_1)\to Y$.

Back to the proof. By fact we have $\mathbb{P}(V/W)$ be the zero locus of \[W\otimes\mathscr{O}_{\mathbb{P}(V)}\hookrightarrow V\otimes\mathscr{O}_{\mathbb{P}(V)}\twoheadrightarrow\mathscr{O}_{\mathbb{P}(V)}(1)\] and so $h^{-1}(\mathbb{P}(V/W))$ be the zero locus of \[W\otimes\mathscr{O}_{B}\hookrightarrow V\otimes\mathscr{O}_{B}\twoheadrightarrow h^* \mathscr{O}_{\mathbb{P}(V)}(1)=\mathscr{L}.\] Similarly $E$ be the zero locus of \[g^* \mathscr{O}_{\mathbb{P}(W)}(1)\hookrightarrow g^* \mathscr{E}\twoheadrightarrow\mathscr{L}.\] Now we have the following commutative diagram: Hence as the left vertical map is surjective, then these two zero loci are the same! $\blacksquare$

Theorem 3. $h$ is the blowing up $\mathrm{Bl}_{\mathbb{P}(V/W)}\mathbb{P}(V)$ described before and $E:=\mathbb{P}(V/W)\times\mathbb{P}(W)$ be its exceptional divisor. Hence $g\circ h^{-1}$ gives $\phi:\mathbb{P}(V)\backslash \mathbb{P}(V/W)\to\mathbb{P}(W)$.

Proof. WLOG we let $k$ is algebraically closed and omit the general case. Consider the diagram again: Any points $x\in B$ given by a point $y=g(x)\in \mathbb{P}(W)$, i.e., a nonzero map $y:W\to k$ and a nonzero map \[\mathscr{E}_y=\mathscr{O}_{\mathbb{P}(W)}(1)_y\oplus V/W=W/\ker(y)\oplus V/W\to k.\] Also by the definition $h(x)$ given by \[V=W\oplus V/W\twoheadrightarrow W/\ker y\oplus V/W\to k.\] Hence $B$ is the graph of $\phi$, in particuler $h$ is an isomorphism over $\mathbb{P}(V)\backslash \mathbb{P}(V/W)$. Now by Lemma 2, using the universal property of blowing up, we have $h$ factored as $\alpha:B\to \mathrm{Bl}_{\mathbb{P}(V/W)}\mathbb{P}(V)$ and $\mathrm{Bl}_{\mathbb{P}(V/W)}\mathbb{P}(V)\to \mathbb{P}(V)$. Now by Lemma 2 again we know that the exceptional divisor of $\alpha$ is $0$, hence $\alpha$ is an isomorphism. $\blacksquare$

Remark. (a) Let $q\in \mathbb{P}(W)$, then $g^{-1}(q)\subset \mathbb{P}(V)$ is the linear span of $\mathbb{P}(V/W)$ and $q$;

(b) Let $L_1,L_2\subset \mathbb{P}(V)$ are two linear spaces such that $L_1\cap L_2=\emptyset$ and $\dim L_1+\dim L_2=\dim V-1$. We can let $L_1=\mathbb{P}(V/W_1)$ and $L_2=\mathbb{P}(V/W_2)$ such that $W_1\oplus W_2=V$. Then we can also define $\phi_i:\mathbb{P}(V)\backslash L_i\to L_j$ where $i\neq j$.