Some Remarks of the Kollar and Mori's Birational Geometry of Algebraic Varieties II
This blog aim to give some remarks and complete some details in this book (Kollar and Mori’s Birational Geometry of Algebraic Varieties). I will read first five chapters of this book. This is the second blog which about chapter 3.
Previously on these:
Some Remarks of the Kollar and Mori’s Birational Geometry of Algebraic Varieties I.
Chapter 3. Cone Theorems
Section 3.2. Basepoint-free Theorem
Step 1. One may add that we find that log resolution with $\sum_j F_j(\supset\mathrm{Ex}(f)\cup\mathrm{supp}(f_* ^{-1}\Delta))$ is snc divisor. $\blacksquare$
Step 5. As $\sum_j F_j$ is snc, then $F$ is regular (hence smooth here). As $\sum(-cr_j+a_j-p_j)F_j=A-F$ for some $F=F_j$ with \[\min_j(-cr_j+a_j-p_j)=-1\] with unique such $j$ (is $F$), hence $\mathrm{discrep}(F,-A|_F)>-1$ by Corollary 2.31. Hence $(F,-A|_F)$ is a klt pair. $\blacksquare$
Section 3.3. The Cone Theorem
Step 3. Let \[W=\mathrm{closure}\left(\overline{NE}_{K\geq 0}+\sum_{\dim F_L=1}F_L\right)\] and pick such $M\in N_{\mathbb{Z}}^* $ such that $F_M\neq\emptyset$ and $F_M\cap W=\emptyset$ with taking positive value over $W$. Let $\mu$ be the largest such that $H+\mu M$ is nef, then it is not ample with $z\cdot(H+\mu M)=0$ and $z\cdot K<0$. Hence $F_{H+\mu M}$ is not contained in $\overline{NE}_{K\geq 0}$. By Step 2 we get a nef $L$ such that $F_L\subset F_{H+\mu M}$ with $\dim F_L=1$ which is impossible! $\blacksquare$
Step 4. Actually we get quotient $(K<0)\to U\subset\mathbb{P}(N_{\mathbb{R}})$ by $\xi\mapsto [(\xi\cdot K):(\xi\cdot H_1):\cdots :(\xi\cdot H_d)]$ and we showed these $F_L$ is discrete in $U$. Now as $\mathbb{P}(\overline{NE}_{k+\varepsilon H\leq 0})\subset U$ is compact and hence contained finite number of these $F_L$ and so is in $\mathbb{P}(\overline{NE}_{k+\varepsilon H< 0})$. $\blacksquare$
Corollary 3.17, 3.18. We may add $\Delta\geq 0$. $\blacksquare$
Corollary 3.18. The first $E\cdot R\neq0$ follows from the following lemma from L3:
Negativity Lemma. Let $X\to Y$ be a birational projective morphism between normal varieties. If $E$ is any exceptional divisor such that $−E$ is nef, then $E\geq 0$. In particular if $E\geq 0$ is exceptional then $E$ is nef if and only if $E = 0$. $\blacksquare$
Add a new corollary! Let $(X,\Delta)$ is a projective klt pair and $F\subset\overline{NE}(X)$ be a $(K_X+\Delta)$-negative extremal face with contraction $g_F:X\to Z$. Then in derived category we have $Rg_{F,* }\mathscr{O}_X\cong\mathscr{O}_Z$.
Proof. We just show that $R^ig_{F,* }\mathscr{O}_X=0$ for $i>0$. As $-(K_X+\Delta)$ is $g_F$-ample, by relative Kawamata–Viehweg vanishing theorem for klt pairs (see Lecture15) well done. $\blacksquare$
Section 3.4. The Rationality Theorem
Step 1. We need to check that the new $H’$ is also nef and big! Here we need to choose appropriate coefficients $m\gg c\gg d > 0$. First we let $r(H)>0$ (or the theorem is obvious), then $H’$ is big by the openness of bigness when $c\gg d > 0$. For the nefness, we may let $n\in\mathbb{N}$ with $H+\frac{1}{n}(K_X+\Delta)$ is nef, hence so is $naH+a(K_X+\Delta)$. As $nH=nH+(K_X+\Delta)-(K_X+\Delta)$ is nef and big, by basepoint-free theorem the linear series $|b(naH+a(K_X+\Delta))|$ is free. Let $d=1,m=b,c=na$ and well done. $\blacksquare$
Step 4. Here we deal with this claim: Claim. For $(p,q)$ sufficiently large and $0 < aq-rq < \varepsilon$, then $L(p,q):=\mathrm{Bs}(|pH+qa(K_X+\Delta)|)$ stable.
The diagram here is not very clear, which leads me astray. Here I redraw a new clearer diagram:
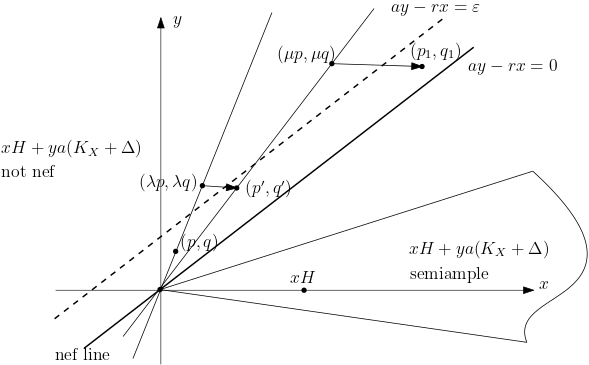
We need to go through the following process with this diagram:
(I) First, pick some $(p,q)$ in the strip. If $(p’,q’)$ large enough, then one can take $(\lambda p,\lambda q)$ and draw an arrow to $(p’,q’)$. Note that $xH$ is semiample now! Hence we can let the direction of this arrow in that semiample cone and the length of the arrow is base-point free! Hence \[p’H+q’a(K_X+\Delta)=\lambda pH+\lambda qa(K_X+\Delta)+\mathrm{free}.\] As $L(\lambda p,\lambda q)\subset L(p,q)$, we get $L(p’,q’)\subset L(\lambda p,\lambda q)\subset L(p,q)$.
(II) Second, let $(p_1,q_1)$ far from $(p’,q’)$ and do the same thing in the first step, then we get $L(p_1,q_1)\subset L(p’,q’)$. Repeat this and using the Noetherian condition, we get a sequence of stable base locuses equal to $L_0$.
(III) Finally, pick two adjacent pairs $(p_n,q_n)$ and $(p_{n+1},q_{n+1})$ in (II) with stable base locuses $L_0$. Hence for any $(p_0,q_0)$ in the strip larger than $(p_{n+1},q_{n+1})$, we can do the same process in (I) with $(p_n,q_n)$ and $(p_0,q_0)$ and get $L(p_0,q_0)=L_0$. So we can let $(p_{n+1},q_{n+1})$ be the thresfold of sufficiently large in the Claim! Well done! $\blacksquare$
Section 3.5. The Non-vanishing Theorem
Step 2. They claim that the number of conditions on $M(q,e)\in|e(qD+G-K_X)|$ that $\mathrm{mult}_x M(q,e)>2de$ is at most \[\frac{e^d}{d!}(2d)^d+\mathcal{O}(e^{d-1}).\]
In the original paper: Actually consider the blowing up $\mathrm{Bl}_xX\to X$ with exceptional divisor $E\cong\mathbb{P}^{d-1}$. Therefore, passing through $x$ imposes $1$ condition, passing through $x$ with multiplicity $2$ imposes a further $d$ conditions,…, and passing through $x$ with multiplicity $l$ imposes a further $\binom{l+d-2}{d-1}$ conditions. Therefore passing through $x$ with multiplicity $l$ imposes a total of $\binom{l+d-1}{d}$ conditions.
Now I will give a more clear explanation of these (taken from birgeom): Let $D$ be a Cartier divisor on a smooth variety $X$, and $x\in X$ a point. Moreover, suppose that $\{h_1,…,h_n\}$ is a basis of $H^0(X,D)$ over $\mathbb{C}$. So $\forall h\in H^0(X,D)$ we have unique expression $h=\sum_i a_ih_i$ where we can assume that all the $h_i$ are regular at $x$ (maybe after changing $D$ in its linear system). So, $h_i$ can be described as polynomials in $d$ variables $t_1, . . . , t_d$ near $x$. Thus, to give $(h)_0=(h) + D\geq 0$ of multiplicity $>l$ at $x$ is the same as giving $h$ with multiplicity $>l$ with respect to $tj$. In particular, we have at most \[\sharp\{\deg \mathrm{monomials}\leq l\}=\frac{l^d}{d!}+\mathcal{O}(l^{d-1})\] conditions to check. That is, there at most codimension $\frac{l^d}{d!}+\mathcal{O}(l^{d-1})$ in $H^0(X,D)$ mains multiplicity $>l$. $\blacksquare$
Section 3.7. Running the MMP
A comment of 3.31.2.(1). Let $f:X\to Y$ be a projective contraction between normal varieties with $\rho(X/Y) = 1$. Assume that the exceptional locus of $f$ contains a divisor, then $f$ is the contraction of a unique irreducible divisor. See MMP Lemma 2.5.7 for the proof. $\blacksquare$
A comment of 3.31.2.(2). If we get a $(K_X+\Delta)$-flipping contraction $f:X\to Y$, why we need to get the flip $f^+:X^+\to Y$ instead of $(Y,f_* \Delta)$? Actually in this case $K_Y+f_* \Delta$ is not $\mathbb{Q}$-Cartier! Indeed, if it is, as $K_X+\Delta=f^* (K_Y+f_* \Delta)$ as $f$ is small, then we have some $f$-contracted curve $l$ such that \[0>(K_X+\Delta)\cdot l=f^* (K_Y+f_* \Delta)\cdot l=0\] which gives a contradiction! $\blacksquare$
Lemma 3.38. The proof after the Lemma 3.41. After taking the complete intersection $S$ of $n-2$ hypersurfaces in normal affine variety $Y$, they claim that $S$ is again a normal surface. Why? Actually this follows from the following results taken from Theorem 3.2 in Arxiv:1912.09076:
Theorem. (Bertini type theorem for normality). Assume that $X$ is an $(R_a +S_b)$-scheme over infinite field $k$ for some $a, b\geq 0$ and $Z\subset\mathbb{P}^n_k$ be a closed subscheme such that $Z\cap X$ is a reduced finite subscheme contained in $X_{reg}$. Then there exists a general hypersurface $H\subset\mathbb{P}^n_k$ containing $Z$ satisfies $X_{reg}\cap H$ is regular and $X\cap H$ is an $(R_a +S_b)$-scheme.
Then using the $R_1+S_2$ for normality, well done! $\blacksquare$
Lemma 3.40. They claim that $H^0(Y,\mathscr{O}_Y(nD+H))\subset H^0(X,\mathscr{O}_X(f_* (nD+H)))$ where $D$ be a combination of exceptional divisors of a resolution $f:Y\to X$. Let $F:=nD+H$ and let $f|_{Y^0}:Y^0\to X^0$ be the isomorphism, then we have
\begin{align*} H^0(Y,\mathscr{O}_Y(F))&=\{g\in K(Y):F+(g)\geq 0\}\\ &\subset\{g\in K(Y^0):F|_{Y^0}+(g)\geq 0\}\\ &=\{g\in K(X^0):F|_{X^0}+(g)\geq 0\}\\ &=\{g\in K(X):f_*F+(g)\geq 0\}\\ &=H^0(X,\mathscr{O}_X(f_*F)), \end{align*}
well done. $\blacksquare$
More on Lemma 3.40. Let $f:X\dashrightarrow Y$ be a small birational map of normal varieties and $D$ a Weil divisor, then $f_* \mathscr{O}_X(D)\cong\mathscr{O}_Y(f_* D)$. In particular $H^0(\mathscr{O}_X(D))\cong H^0(\mathscr{O}_Y(f_* D)$.
Indeed, we just need to show $H^0(\mathscr{O}_X(D))\cong H^0(\mathscr{O}_Y(f_* D)$. We just deal with the line bundle case. Locally this is just Hartogs’s theorem. To gluing them up, we find that locally the restriction map on $\mathscr{O}_U$ to a dense open subset is always injective as it is integral and the sections of $\mathscr{O}_X$ can be viewed as morphisms to $\mathbb{A}^1$ and the latter is separated (hence we get the uniqueness of the maps)! Well done.
Of course we can do it directly for the general case as previous method. $\blacksquare$
A fundamental result about the flips. Let $f:X\to Y$ be a flipping contraction for a dlt pair $(X,\Delta)$ with $\mathbb{Q}$-divisor $\Delta$. The flip $f^+$ exists, if and only if $\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)$ is a finitely generated $\mathscr{O}_Y$-algebra. We then have that \[X^+ \cong\underline{\mathrm{Proj}}_Y\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor).\]
Proof. If the flip $f^+$ exists we get $X\dashrightarrow X^+$ is small and $K_{X^+}+\Delta^+$ is $f^+$-ample, then we get \[\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)\cong\bigoplus_{m\geq 0} f^+_* \mathscr{O}_{X^+}(\lfloor m(K_{X^+}+\Delta^+)\rfloor)\] and the right-hand side is a finitely generated sheaf of $\mathscr{O}_Y$-algebras. Finally we have $X^+ \cong\underline{\mathrm{Proj}}_Y\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)$ as it is proper.
Conversely, let $\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)$ is a finitely generated $\mathscr{O}_Y$-algebra. Let $X^+:=\underline{\mathrm{Proj}}_Y\bigoplus_{m\geq 0} f_* \mathscr{O}_X(\lfloor m(K_X+\Delta)\rfloor)$ and claim that $f^+:X^+\to Y$ is the flip. Here we just give a sketch and we refer Proposition 5.21 in [CHDAV10]1 or Theorem 9-1-2 in [Mori02]2. WLOG we let $K_X+\Delta$ is of integral coeffecient as it is $\mathbb{Q}$-divisor. If $E$ is a $f^+$-exceptional divisor and as for some $m\gg0$ we have \[f^+_* \mathscr{O}_{X^+}(1)\cong f_* \mathscr{O}_X(m(K_X+\Delta))\cong \mathscr{O}_Y(m(K_Y+f_* \Delta)),\] hence for any $t\gg0$ we get\[\mathscr{O}_Y(tm(K_Y+f_* \Delta))\cong f^+_* \mathscr{O}_{X^+}(t)\subset f^+_* \mathscr{O}_{X^+}(t)(E)\] where the last inclusion is strict. As $E$ is $f^+$-exceptional and sheaf $\mathscr{O}_Y(tm(K_Y+f_* \Delta))$ is reflexive. Hence $f^+$ is small. Others are omitted. $\blacksquare$
More Things. Bhatt and Lurie proved a version of the Riemann-Hilbert correspondence in positive characteristic. Bhatt proved the Cohen-Macaulayness of the integral closure of an excellent Noetherian domain. Using these techniques and results, MMP has recently been generalized in two different directions:
-
- In dimension $3$ in mixed characteristic (essentially over $\mathrm{Spec}\mathbb{Z}$) by Bhatt-Ma-PatakfalviSchwede-Tucker-Waldron-Witaszek;
-
- In characteristic $0$, most of the MMP works over an excellent $\mathbb{Q}$-scheme by Murayama-Lyu. $\blacksquare$
Section 3.8. Minimal and Canonical Models
Corollary 3.53. Here we explain how we use effectivity of $E$. Here we follows Lemma 7.11 and some comments in 7.12 in [HDAG01]3.
- Let $f:X\to Y$ be a proper birational map between varieties with $Y$ normal. Let $D$ be a Cartier divisor on $Y$ and $E$ is effective $f$-exceptional divisor on $X$, then we have $H^0(Y,D)\cong H^0(X,f^* D+E)$. Hence in particular we have $f_* \mathscr{O}_X(E)\cong\mathscr{O}_Y$.
Proof. As we have \[H^0(Y,D)\subset H^0(X,f^* D)\subset H^0(X,f^* D+E)\subset H^0(X\backslash\mathrm{Ex}(f),f^* D+E)\] and isomorphisms \[H^0(X\backslash\mathrm{Ex}(f),f^* D+E)\cong H^0(X\backslash\mathrm{Ex}(f),f^* D)\cong H^0(Y\backslash f(\mathrm{Ex}(f)),D)\cong H^0(Y,D)\] as $\mathrm{codim}_Yf(\mathrm{Ex}(f))\geq2$. Hence well done. $\blacksquare$
Remark. (1) For some kind of converse, see the comments of Corollary 5.24 in KMIII;
(2) I don’t know whether this lemma is right for general divisor $D$ or not. Actually I’m not sure if the projection formula holds for reflexive rank $1$-module (or more precisely, injective object tensoring a reflexive rank $1$-module is always an injective object?). $\blacksquare$
Corollary 3.54. Here by (3.53) we can get $X_i$ are canonical models of $K_{X_i}$ are $f_i$-ample, respectively. But why we assume $f_i$-nef and $X_i$ is of minimal model by (3.53)? I don’t know what’s going on.